Herbie reports


The Herbie report, which is output by the Herbie web commands, lists five items.
First, a brief summary of the results. For most uses, the “Average Error” number, which summarizes how accurate the input and output expressions are, is the most important number in this section. The other numbers are: the time Herbie took to improve the program; the precision Herbie assumed floating-point operations (which can be set at the command line); and the internal precision used to ensure accurate results.

Second, the input and output programs themselves.
These are printed in standard mathematical syntax.
Library functions not often used by mathematicians,
including atan2, expm1,
fma, hypot, lgamma,
log1p, and logb
are drawn with a sub- or super-script asterisk,
while if statements are rendered as in a program.

Third, under Error, a graph of floating-point error
versus input value. This is helpful for understanding the sorts of
inputs Herbie is improving accuracy on. Sometimes, Herbie improved
accuracy on some inputs at the cost of accuracy on other inputs
that you care more about. In these cases, you can add
a :precondition to restrict the inputs Herbie reasons
about.
On these graphs, the red line is the error of the input program,
while the blue line is the error of the output program
(both can be toggled).
For expressions with multiple variables,
the variable on the horizontal axis can be selected.
If Herbie decided to insert
an if statement into the program,
the locations of those if statements
will be marked with vertical bars.
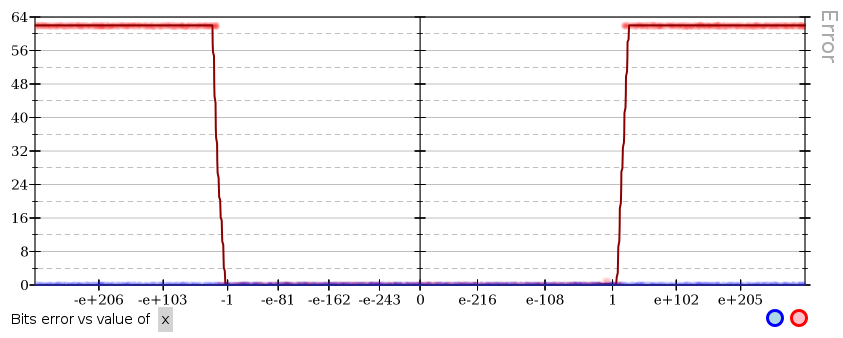
x is selected) and the toggles for the
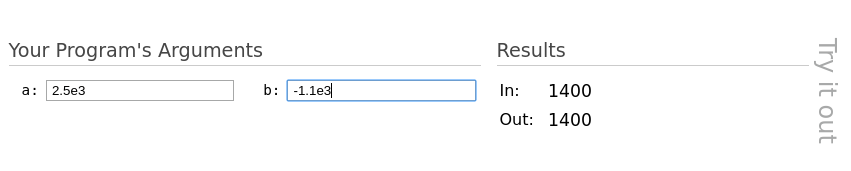
input and output program (both are toggled on).Fourth, a form where you can try out specific inputs on the input program and Herbie's output program. Enter the argument values on the left, and the input and output programs will be evaulated on those arguments and the results printed on the right.
Fifth, a derivation of the output from the input. For complex or unexpected programs, these can be helpful. Each substantive step in the derivation also lists the error, in bits, of that step's output.
The derivations may name rules built into Herbie, or may claim derivation steps are done by simplification, series expansion, or other Herbie strategies. The derivation will also call out splits of the input into regimes, and strategies Herbie is invoking. When one part of the term is colored blue, that is the only part of the term modified by the operation.

Sixth and finally, a breakdown of Herbie's runtime. This can usually be ignored. The colored bar is a timeline of Herbie's run, with each section of the bar sized proportionally to its runtime, and each color corresponding to a strategy; hover over that section of the bar to learn which strategy.
If you find a bug, include the code snippet in this section when filing the bug. Please also include the debug log linked from this block.

We expect the report to grow more informative with future versions. Please get in touch if there is more information you'd like to see.