Herbie Tutorial

Herbie rewrites floating point expressions to make them more accurate. Floating point arithmetic is inaccurate; even 0.1 + 0.2 ≠ 0.3 for a computer. Herbie helps find and fix these mysterious inaccuracies.

To get started, download and install Herbie. You're then ready to begin using Herbie.

Giving Herbie expressions

Start Herbie with:

herbie web

After a brief wait, this will open your web browser and show you Herbie's main window. The most important part of the page is this bit:

Type (1 + x) - x into this box and press enter. You should see the entry box gray out, then some text appear on the screen describing what Herbie is doing. After a few seconds, you'll be redirected to a page with Herbie's results. The most important part of that page is the large gray box in the middle:

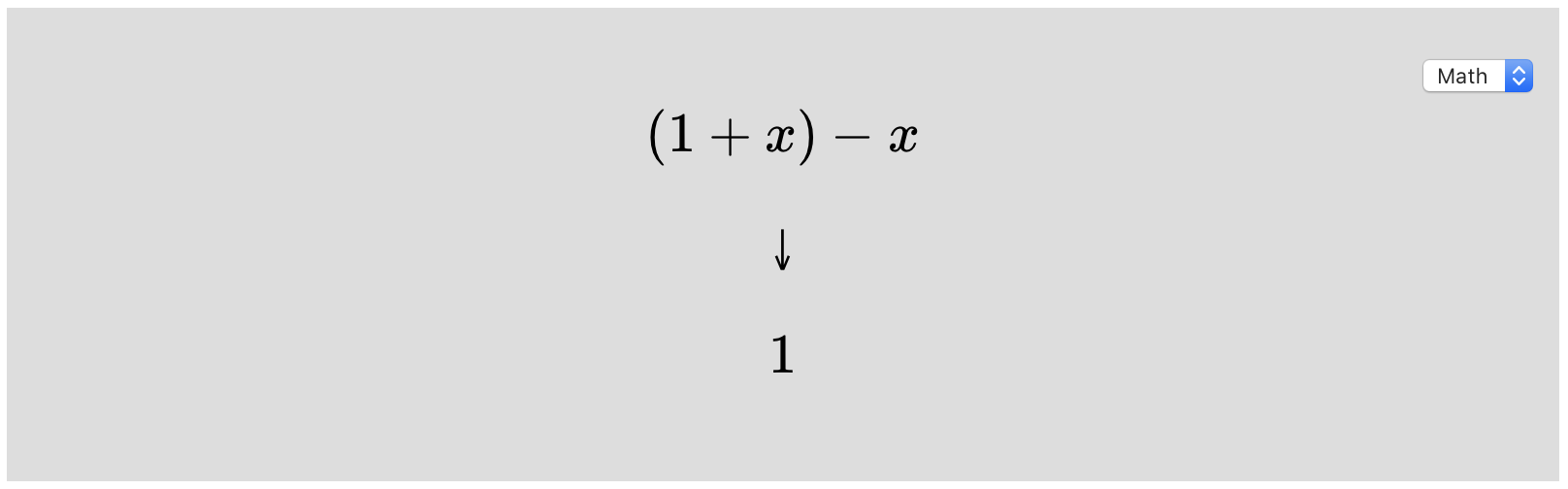
It shows the input, (1 + x) - x, and Herbie's more accurate way to evaluate that expression: 1. Herbie did a good job, which you can see from the statistics at the top of the page:

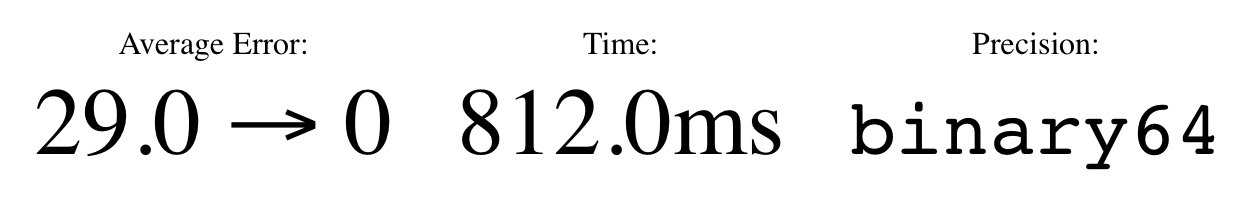
The initial program had 29.4 bits of error (on average), while Herbie's better version had 0 bits of error. That's because (1 + x) - x should always be exactly equal to 1, but in floating-point arithmetic, when x is really big, 1 + x rounds down to x and the expression returns 0.

There's lots more information on this results web page, which you can use explain more about the expression's errors and how Herbie derived its result.

Programming with Herbie

Now that you've run Herbie and know how to read its results, let's apply Herbie to a realistic program.

Herbie's input expressions can come from source code, mathematical models, or even a debugging tool like Herbgrind. But most often, they come from your mind, while you're writing new mathematical code.

When you're writing a new numerical program, it's best to keep Herbie open in a browser tab so you can run it easily. That way, you can run Herbie on any complex floating-point expression you're coding up and so always use an accurate version of that expression. Herbie has options to log all the expressions you enter, so that you can refer to them later.

However, let's suppose you're instead tracking down a floating-point bug in existing code. Then you'll need start by identifying the problematic floating-point expression.

To demonstrate the workflow, let's walk through bug 208 in math.js, a math library for JavaScript. The bug deals with inaccurate square roots for complex numbers. (For a full write-up of the bug itself, check out a blog post by one of the Herbie authors.)

Finding the problematic expression

In most programs, there's a small core that does the mathematical computations, while the rest of the program sets up parameters, handles control flow, visualizes or print results, and so on. The mathematical core is what Herbie will be interested in.

For our example, let's start in lib/function/. This directory contains many subdirectories; each file in each subdirectory defines a collection of mathematical functions. The bug we're interested in is about complex square root, which is defined in arithmetic/sqrt.js.

This file handles argument checks, five different number types, and error handling, for both real and complex square roots. None of that is of interest to Herbie; we want to extract just the mathematical core. So skip down to the isComplex(x) case:

var r = Math.sqrt(x.re * x.re + x.im * x.im);
if (x.im >= 0) {
  return new Complex(
      0.5 * Math.sqrt(2.0 * (r + x.re)),
      0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}
else {
  return new Complex(
      0.5 * Math.sqrt(2.0 * (r + x.re)),
      -0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}

This is the mathematical core that we want to send to Herbie.

Converting problematic code to Herbie input

In this code, x is of type Complex, a data structure with multiple fields. Herbie only deals with floating-point numbers, not data structures, so we will treat the input x as two separate inputs to Herbie: xre and xim. We'll also pass each field of the output to Herbie separately.

This code also branches between non-negative x.im and negative x.im. It's usually better to send each branch to Herbie separately. So in total this code turns into four Herbie inputs: two output fields, for each of two branches.

Let's focus on first field of the output for the case of non-negative x.im.

The variable r is an intermediate variable in this code block. Intermediate variables provide Herbie with crucial information that Herbie can use to improve accuracy, so you want to expand or inline them. The result looks like this:

0.5 * sqrt(2.0 * (sqrt(xre * xre + xim * xim) + xre))

Recall that this code is only run when x.im is non-negative. So, before running Herbie on this expression, click the “Additional options” link, and enter xim >= 0 for the precondition. This asks Herbie to consider only non-negative values of xim when improving the accuracy of this expression.

Using Herbie's results

Herbie will churn for a few seconds and produce an output, perhaps something like this:

Herbie's algorithm is randomized, so you likely won't see the exact same thing. For example, the branch expression xre ≤ -4.780438341784697e-111 will probably have some other really small number. And perhaps Herbie will choose slightly different expressions. But the result should be recognizably similar. In this case, Herbie reports that the initial expression had 38.7 bits of error, and that the output has 29.4.

It's a little harder to describe what Herbie found wrong with the original expression, and why its new version is better—it is due to a floating-point phenomenon called “cancellation”. But you can get some insight from the error plot just below the program block. Select the xim variable just below the plot, and you will see something like this:

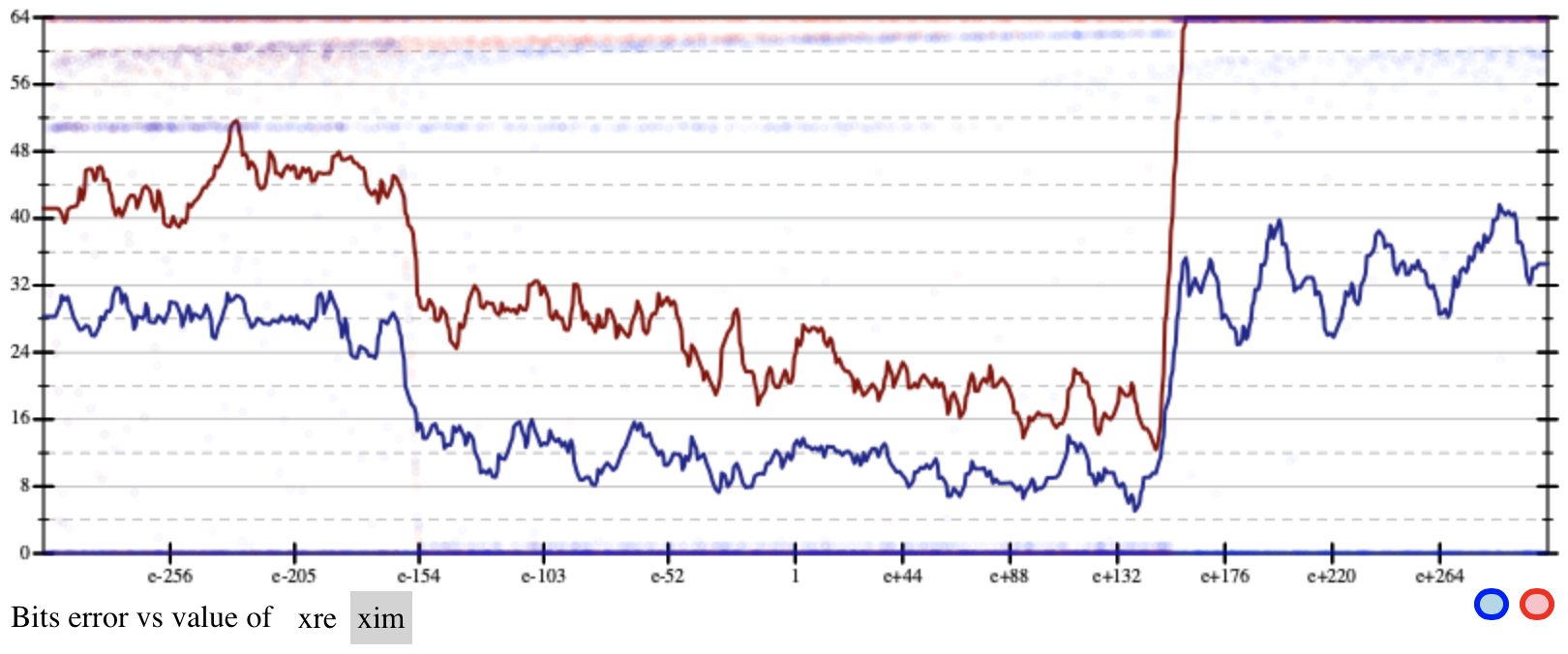
There's a lot going on here. Along the horizontal axis, you have the various values of xim. Note that the graph is log-scale, and includes only non-negative values thanks to our precondition. The value 1 is in the middle; to the left are values with small exponents close to zero, and to the right you have values with large exponents approaching infinity.

The vertical axis measures bits of error, from 0 to 64. Lower is better. There are two lines drawn: a red one for the original expression and a blue one for Herbie's version. You can see from the plot that as xim gets smaller (toward the left, closer to zero), Herbie's improvement becomes more and more significant. You can also see that for very large values of xim, the original program had maximal error (in fact, it overflows) but the Herbie's version is better, though not great.

Of course, your exact output will differ a bit from the screenshots and descriptions here, because Herbie is randomized.

Now that you have the more accurate version of this expression, all you need to do is insert it back into the program:

var r = Math.sqrt(x.re * x.re + x.im * x.im);
// Herbie version of 0.5 * Math.sqrt(2.0 * (r + x.re))
var re;
if (x.re <= -4.780438341784697e-111) {
    re = Math.abs(x.im) * Math.sqrt(0.5) / Math.sqrt(r - x.re);
} else if (x.re <= 1.857088496624289e-105) {
    re = 0.5 * Math.sqrt(2.0 * (x.re + x.im));
} else if (x.re <= 117.16871373388169) {
    re = 0.5 * Math.sqrt(2.0 * (r + x.re));
} else if (x.re <= 5.213930590364927e+88) {
    re = 0.5 * Math.sqrt(2.0 * (x.re + x.im));
} else {
    re = 0.5 * Math.sqrt(2.0 * (x.re + x.re));
}
if (x.im >= 0) {
  return new Complex(
      re,
      0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}
else {
  return new Complex(
      0.5 * Math.sqrt(2.0 * (r + x.re)),
      -0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}

Note that I've left the original code in place in a comment. As Herbie gets better, you can re-run it on this original expression to see if it comes up with improvements in accuracy.

By the way, for some languages, like C, you can use the drop-down in the top-right corner of the gray program block to translate Herbie's output to that language.

Next steps

With this change, we've made this part of the complex square root function much more accurate, and we could repeat the same steps for the other branches and other fields in this program. You now have a pretty good understanding of Herbie and how to use it. Please let us know if Herbie has helped you, and check out the documentation to learn more about Herbie's various options and outputs.