Herbie Tutorial

Herbie rewrites floating point expressions to make them more accurate. Floating point arithmetic is inaccurate; even 0.1 + 0.2 ≠ 0.3 in floating-point. Herbie helps find and fix these mysterious inaccuracies.
To get started, download and install Herbie. You're then ready to begin using it.
Start Herbie with:
herbie web
After a brief wait, your web browser should open and show you Herbie's main window. The most important part of the page is this bit:

Let's start by just looking at an example of Herbie running.
Click "Show an example". This will pre-fill the expression
sqrt(x + 1) - sqrt(x)
with x ranging from to 0 and 1.79e308.
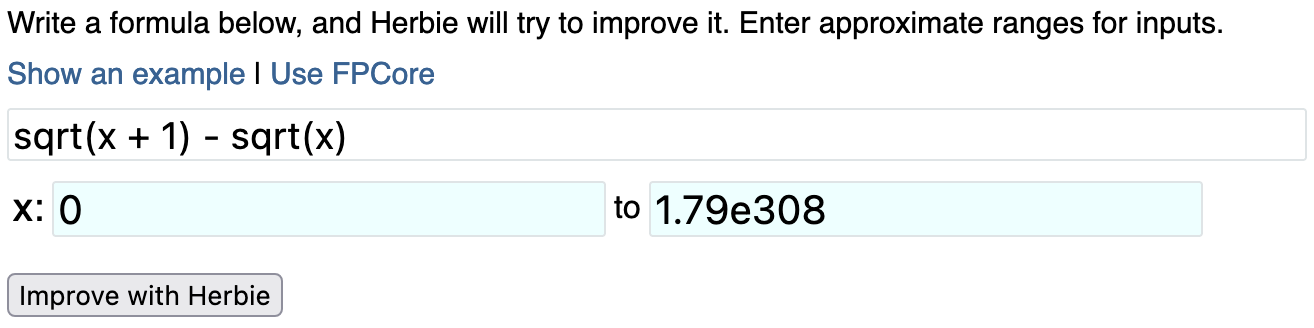
Now that you have an expression and a range for each variable, click the "Improve with Herbie" button. You should see the entry box gray out, and shortly thereafter some text should appear describing what Herbie is doing. After a few seconds, you'll be redirected to a page with Herbie's results.
The very top of this results page gives some quick statistics about the alternative ways Herbie found for evaluating this expression:

Here, you can see that Herbie's most accurate alternative has an accuracy of 99.7%, much better than the initial program's 53.2%, and that in total Herbie found 5 alternative. One of those alternatives is both more accurate than the original expression and also 1.9× faster. The rest of the result page shows each of these alternatives, including details like how they were derived. These details are all documented, but for the sake of the tutorial let's move on to a more realistic example.
You can use Herbie on expressions from source code, mathematical models, or debugging tools. But most users use Herbie as they write code, passing any complex floating-point tool to Herbie as they go. Herbie has options to log all the expressions you enter so that you can refer to them later.
But to keep the tutorial focused, let's suppose you're instead tracking down a floating-point bug in existing code. Then you'll need to start by identifying the problematic floating-point expression.
To demonstrate the workflow, let's walk through bug 208 in math.js, a math library for JavaScript. The bug deals with inaccurate square roots for complex numbers. (For a full write-up of the bug itself, check out a blog post by one of the Herbie authors.)
In most programs, there's a small core that does the mathematical computations, while the rest of the program sets up parameters, handles control flow, visualizes or prints results, and so on. The mathematical core is what Herbie will be interested in.
For our example, let's start
in lib/function/.
This directory contains many subdirectories; each file in each
subdirectory defines a collection of mathematical functions. The
bug we're interested in is about complex square root, which is
defined in
arithmetic/sqrt.js.
This file handles argument checks, five different number types,
and error handling, for both real and complex square roots. None
of that is of interest to Herbie; we want to extract just the
mathematical core. So skip down to the isComplex(x)
case:
var r = Math.sqrt(x.re * x.re + x.im * x.im);
if (x.im >= 0) {
return new Complex(
0.5 * Math.sqrt(2.0 * (r + x.re)),
0.5 * Math.sqrt(2.0 * (r - x.re))
);
}
else {
return new Complex(
0.5 * Math.sqrt(2.0 * (r + x.re)),
-0.5 * Math.sqrt(2.0 * (r - x.re))
);
}
This is the mathematical core that we want to send to Herbie.
In this code, x is of type Complex, a
data structure with multiple fields. Herbie only deals with
floating-point numbers, not data structures, so we will treat the
input x as two separate inputs to
Herbie: xre and xim. We'll also pass
each field of the output to Herbie separately.
This code also branches between non-negative x.im and
negative x.im. It's usually better to send each
branch to Herbie separately. So in total, this code turns into four
Herbie inputs: two output fields, for each of the two branches.
Let's focus on the first field of the output for the case of
non-negative x.im.
The variable r is an intermediate variable in this
code block. Intermediate variables provide Herbie with crucial
information that Herbie can use to improve accuracy, so you want to
expand or inline them. The result looks like this:
0.5 * sqrt(2.0 * (sqrt(xre * xre + xim * xim) + xre))
Recall that this code is only run when x.im is
non-negative (but it runs for all values of x.re). So,
select the full range of values for x.re, but restrict
the range of x.im, like this:

xim when improving the accuracy of this
expression.
Herbie will churn for a few seconds and produce a results page. In this case, Herbie found 4 alternatives, and we're interested in the most accurate one, which should have an accuracy of 84.6%:

Below these summary statistics, we can see a graph of accuracy
versus input value. By default, it shows accuracy
versus xim; higher is better:

The drop in accuracy once xim is bigger than
about 1e150 really stands out, but you can also see
that Herbie's alternative more accurate for smaller xim
values, too. You can also change the graph to plot accuracy
versus xre instead:
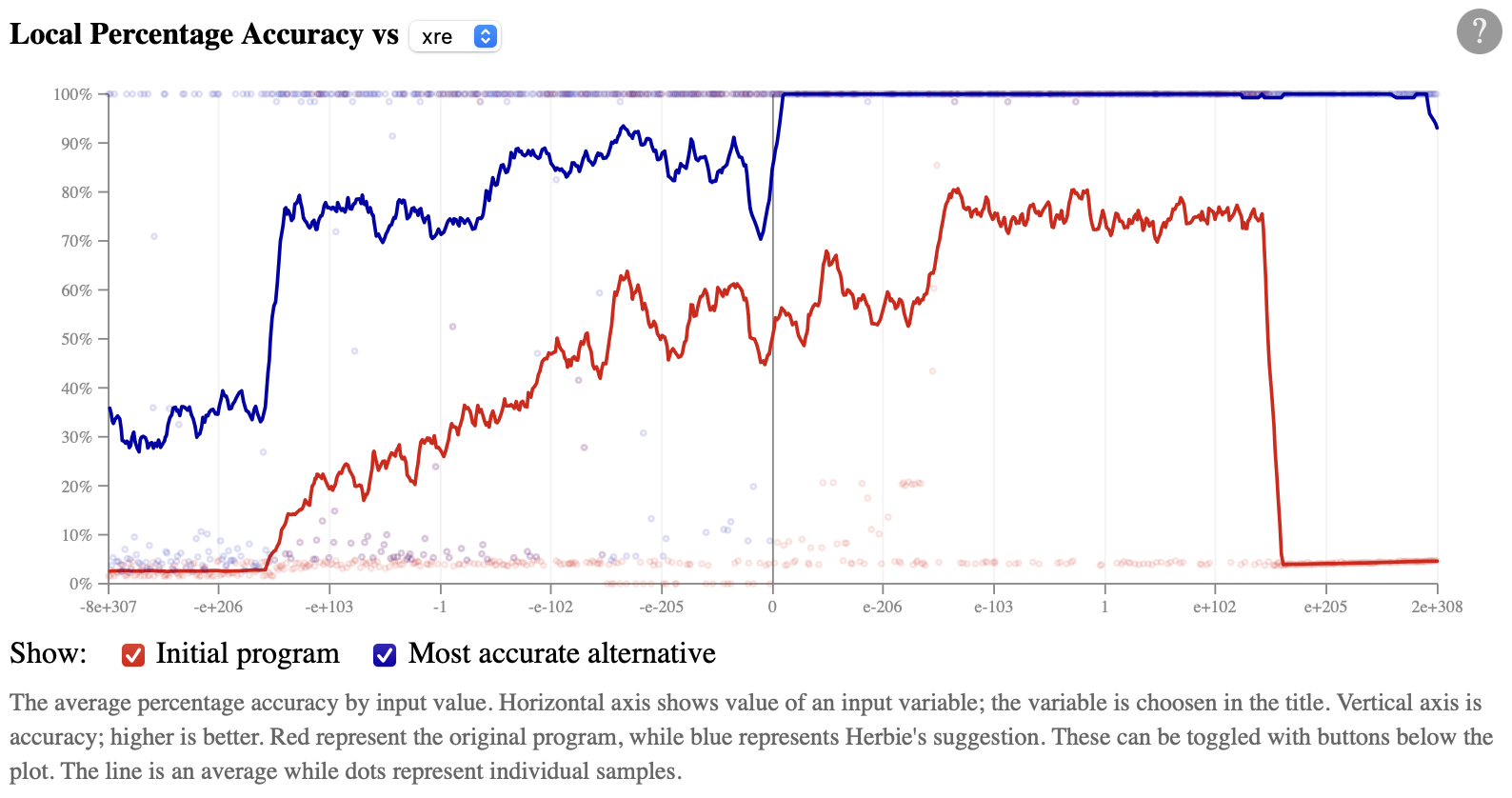
This plot makes it clear that Herbie's alternative is almost
perfectly accurate for positive xre, but still has some
error for negative xre.
Herbie also found other alternatives, which are less accurate but might be faster. You can see a summary in this table:
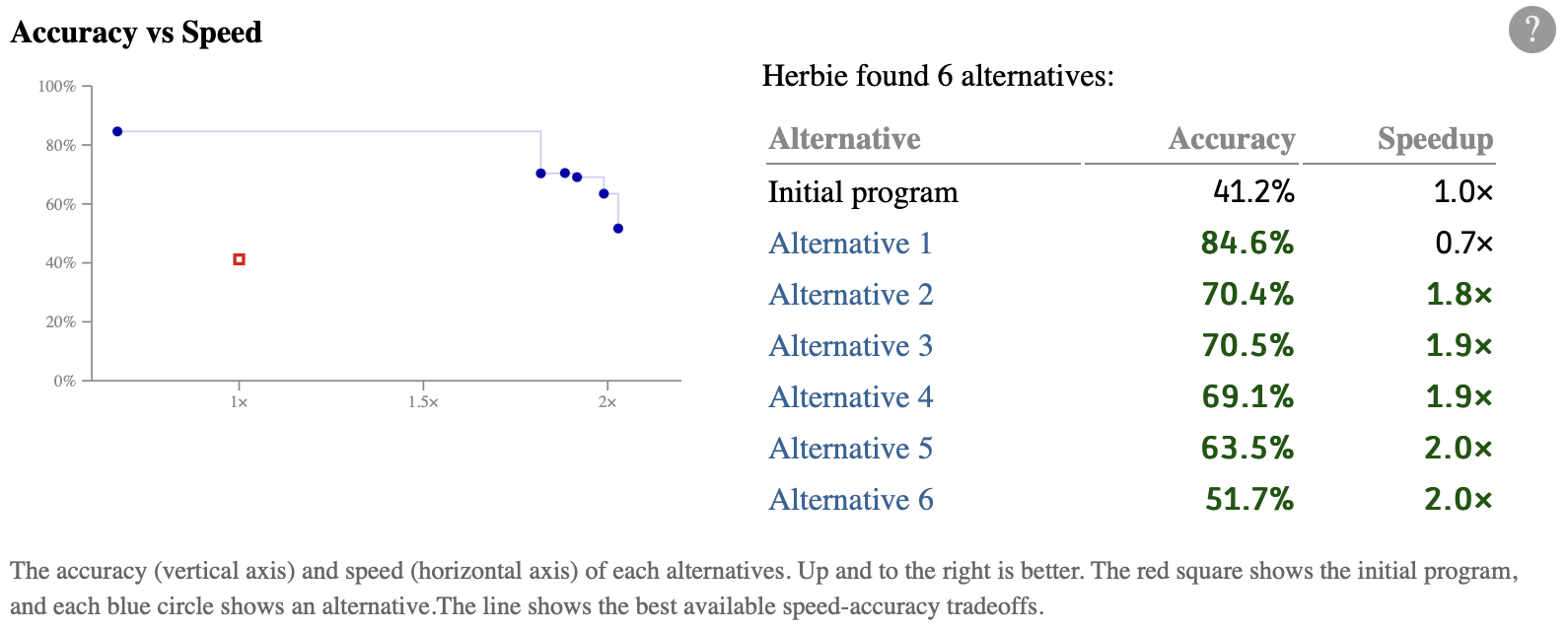
Herbie's algorithm is randomized, so you likely won't see the exact same thing; you might see more or fewer alternatives, and they might be more or less accurate and fast. That said, the most accurate alternative should be pretty similar.
That alternative itself is shown lower down on the page:

A couple features of this alternative stand out immediately.
First of all, Herbie inserted an if statement.
This if statement handles a phenomenon known as
cancellation, and is part of why Herbie's alternative is more
accurate. Herbie also replaced the square root operation with
the hypot function, which computes distances more
accurately than a direct square root operation.
If you want to see more about how Herbie derived this result, you could click on the word "Derivation" to see a detailed, step-by-step explanation of how Herbie did it. For now, though, let's move on to look at another alternative.
The fifth alternative suggested by Herbie is much less accurate, but it is about twice as fast as the original program:

This alternative is kind of strange: it has two branches, and
each one only uses one of the two variables xre
and xim. That explains why it's fast, but it's still
more accurate than the initial program because it avoids
cancellation and overflow issues that plagued the original.
In this case, we were interested in the most accurate possible implementation, so let's try to use Herbie's most accurate alternative.
// Herbie version of 0.5 * sqrt(2.0 * (sqrt(xre*xre + xim*xim) + xre))
var r = Math.hypot(x.re, x.im);
var re;
if (xre + r <= 0) {
re = 0.5 * Math.sqrt(2 * (x.im / (x.re / x.im) * -0.5));
} else {
re = 0.5 * Math.sqrt(2 * (x.re + r));
}
if (x.im >= 0) {
return new Complex(
re,
0.5 * Math.sqrt(2.0 * (r - x.re))
);
}
else {
return new Complex(
0.5 * Math.sqrt(2.0 * (r + x.re)),
-0.5 * Math.sqrt(2.0 * (r - x.re))
);
}
Note that I've left the Herbie query in a comment. As Herbie gets better, you can re-run it on this original expression to see if it comes up with improvements in accuracy.
By the way, for some languages, including JavaScript, you can use the drop-down in the top-right corner of the alternative block to translate Herbie's output to that language. However, you will still probably need to refactor and modify the results to fit your code structure, just like here.
With this change, we've made this part of the complex square root function much more accurate, and we could repeat the same steps for the other branches and other fields in this program. You now have a pretty good understanding of Herbie and how to use it. Please let us know if Herbie has helped you, and check out the documentation to learn more about Herbie's various options and outputs.