Herbie Tutorial

Herbie rewrites floating point expressions to make them more accurate. Floating point arithmetic is inaccurate; even 0.1 + 0.2 ≠ 0.3 in floating-point. Herbie helps find and fix these mysterious inaccuracies.

To get started, download and install Herbie. You're then ready to begin using it.

Giving Herbie expressions

Start Herbie with:

racket -l herbie web

Alternatively, if you added herbie to the path, you can always replace racket -l herbie with just herbie.

After a brief wait, your web browser should open and show you Herbie's main window. The most important part of the page is this bit:

Let's start by just looking at an example of Herbie running. Click "Show an example". This will pre-fill the expression sqrt(x + 1) - sqrt(x) with x ranging from to 0 and 1.79e308.

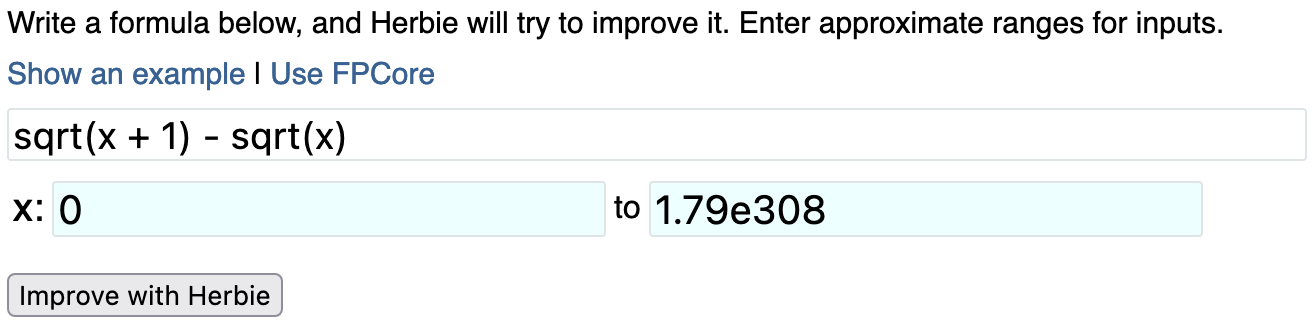
Now that you have an expression and a range for each variable, click the "Improve with Herbie" button. You should see the entry box gray out, and shortly thereafter some text should appear describing what Herbie is doing. After a few seconds, you'll be redirected to a page with Herbie's results.

The very top of this results page gives some quick statistics about the alternative ways Herbie found for evaluating this expression:

Here, you can see that Herbie's most accurate alternative has an accuracy of 99.7%, much better than the initial program's 53.2%, and that in total Herbie found 5 alternatives. One of those alternatives is both more accurate than the original expression and also 1.9× faster. The rest of the result page shows each of these alternatives, including details like how they were derived. These details are all documented, but for the sake of the tutorial let's move on to a more realistic example.

Programming with Herbie

You can use Herbie on expressions from source code, mathematical models, or debugging tools. But most users use Herbie as they write code, asking it about any complex floating-point expression they write. Herbie has options to log all the expressions you enter so that you can refer to them later.

But to keep the tutorial focused, let's suppose you're instead tracking down a floating-point bug in existing code. Then you'll need to start by identifying the problematic floating-point expression.

To demonstrate the workflow, let's walk through bug 208 in math.js, a math library for JavaScript. The bug deals with inaccurate square roots for complex numbers. (For a full write-up of the bug itself, check out a blog post by one of the Herbie authors.)

Finding the problematic expression

In most programs, there's a small kernel that does the mathematical computations, while the rest of the program sets up parameters, handles control flow, visualizes or prints results, and so on. The mathematical core is what Herbie will be interested in.

For our example, let's start in lib/function/. This directory contains many subdirectories; each file in each subdirectory defines a collection of mathematical functions. We're interested in the complex square root function, which is defined in arithmetic/sqrt.js.

This file handles argument checks, different types, and error handling, for both real and complex square roots. None of that is of interest to Herbie; we want to extract just the mathematical core. So skip down to the isComplex(x) case:

var r = Math.sqrt(x.re * x.re + x.im * x.im);
if (x.im >= 0) {
  return new Complex(
      0.5 * Math.sqrt(2.0 * (r + x.re)),
      0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}
else {
  return new Complex(
      0.5 * Math.sqrt(2.0 * (r + x.re)),
      -0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}

This is the mathematical core that we want to send to Herbie.

Converting problematic code to Herbie input

In this code, x is of type Complex, a data structure with multiple fields. Herbie only deals with floating-point numbers, not data structures, so we will treat the input x as two separate inputs to Herbie: xre and xim. We'll also pass each field of the output to Herbie separately.

This code also branches between non-negative x.im and negative x.im. It's usually better to send each branch to Herbie separately. So in total, this code turns into four Herbie inputs: two output fields, for each of the two branches.

Let's focus on the first field of the output for the case of non-negative x.im.

The variable r is an intermediate variable in this code block. Intermediate variables provide Herbie with crucial information that Herbie can use to improve accuracy, so you want to expand or inline them. The result looks like this:

0.5 * sqrt(2.0 * (sqrt(xre * xre + xim * xim) + xre))

Recall that this code is only run when x.im is non-negative (but it runs for all values of x.re). So, select the full range of values for x.re, but restrict the range of x.im, like this:

Herbie's results

Herbie will churn for a few seconds and produce a results page. In this case, Herbie found 4 alternatives, and we're interested in the most accurate one, which should have an accuracy of 84.6%:

Below these summary statistics, we can see a graph of accuracy versus input value. By default, it shows accuracy versus xim; higher is better:

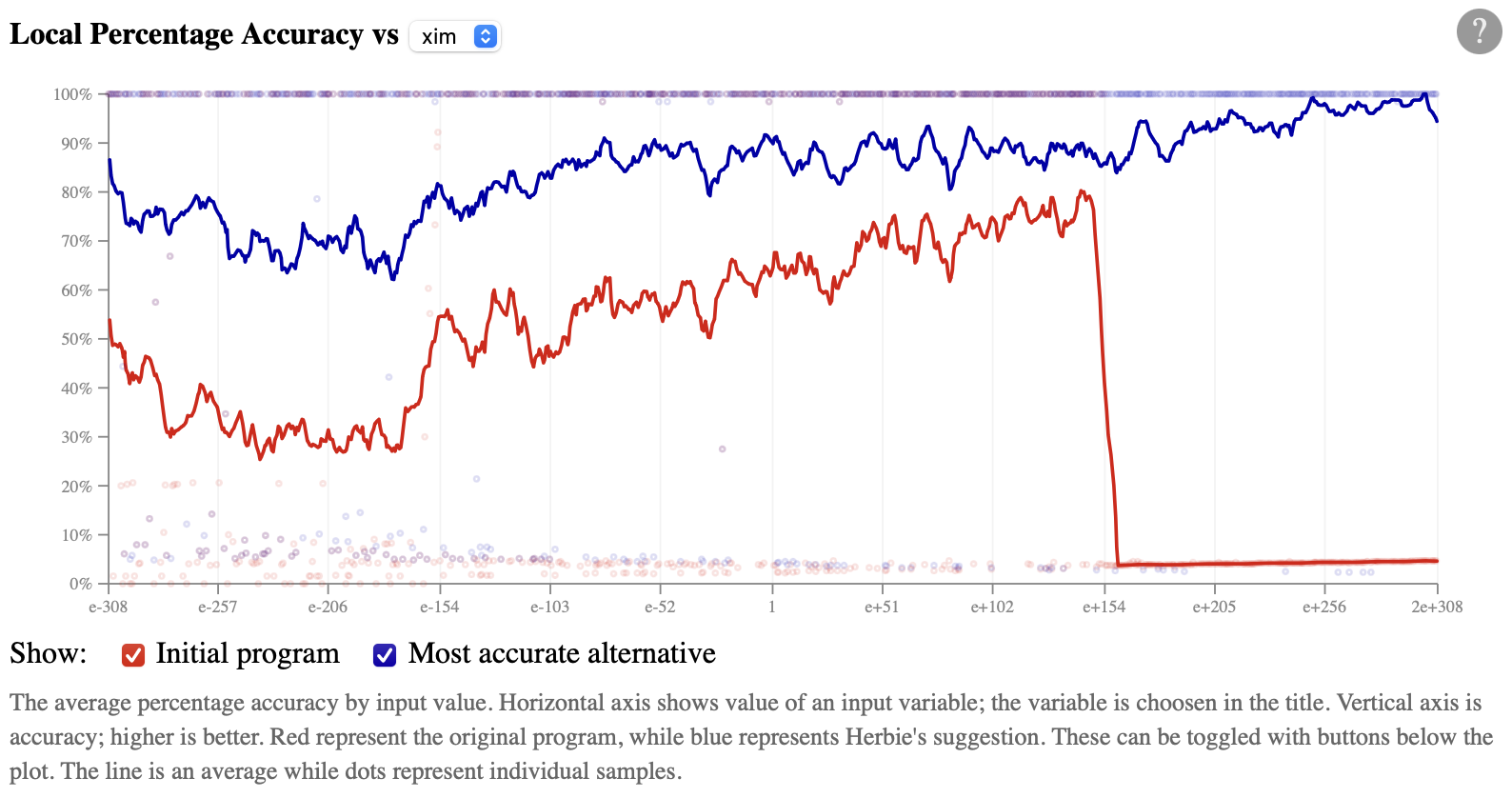
The drop in accuracy once xim is bigger than about 1e150 really stands out, but you can also see that Herbie's alternative more accurate for smaller xim values, too. You can also change the graph to plot accuracy versus xre instead:

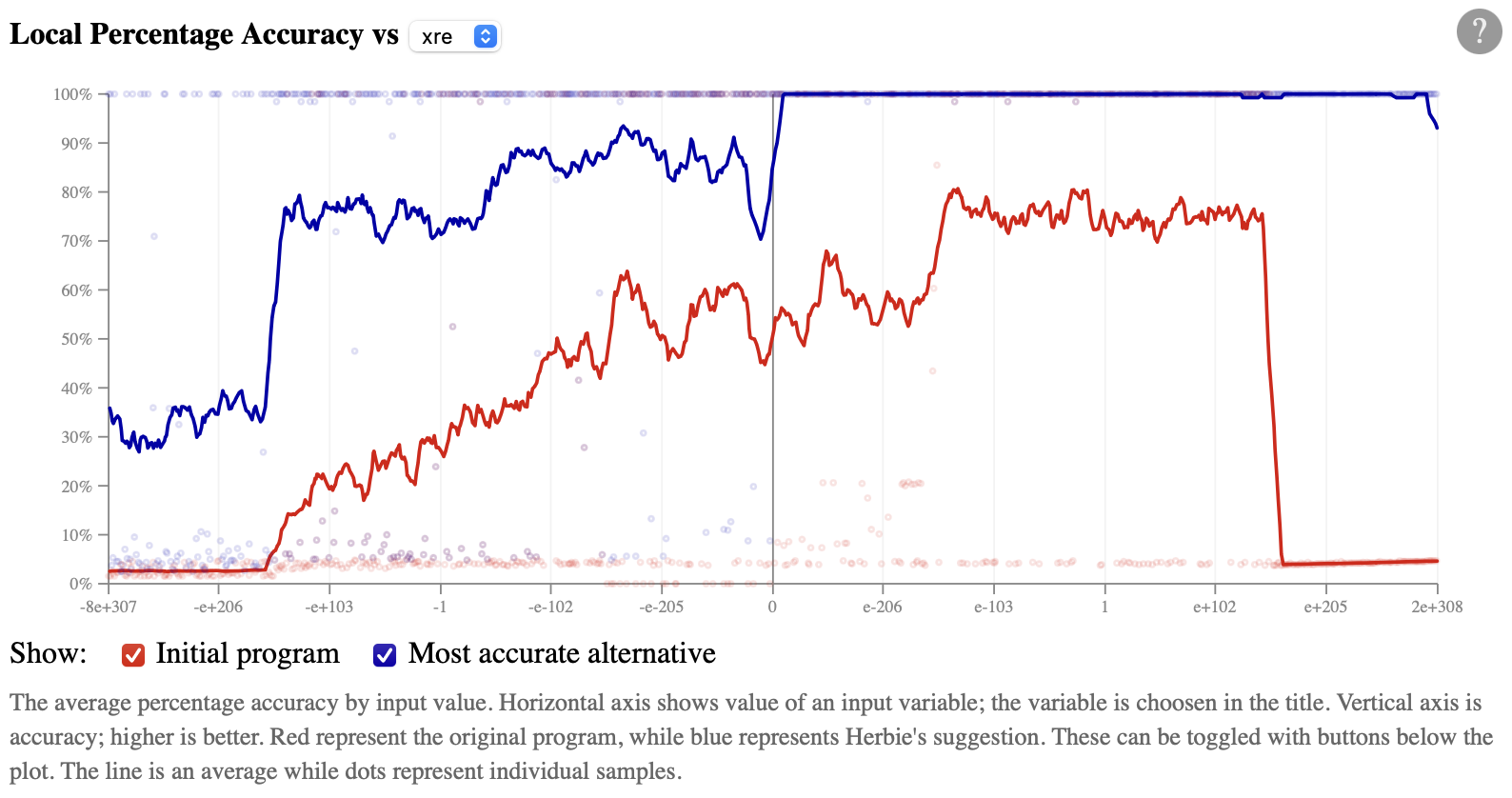
This plot makes it clear that Herbie's alternative is almost perfectly accurate for positive xre, but still has some error for negative xre.

Herbie also found other alternatives, which are less accurate but might be faster. You can see a summary in this table:

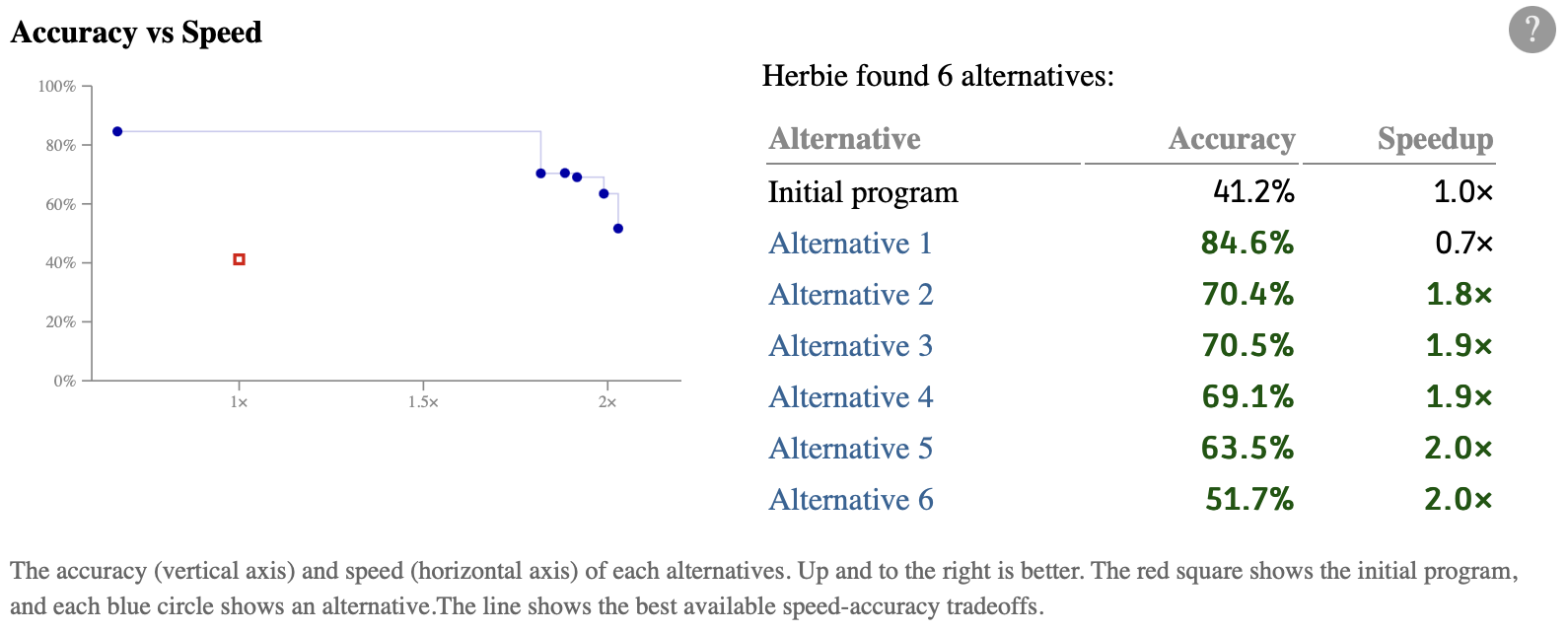
Herbie's algorithm is randomized, so you likely won't see the exact same thing; you might see more or fewer alternatives, and they might be more or less accurate and fast. That said, the most accurate alternative should be pretty similar.

That alternative itself is shown lower down on the page:

A couple features of this alternative stand out immediately. First of all, Herbie inserted an if statement. This if statement handles a phenomenon known as cancellation, and is part of why Herbie's alternative is more accurate. Herbie also replaced the square root operation with the hypot function, which computes distances more accurately than a direct square root operation.

If you want to see more about how Herbie derived this result, you could click on the word "Derivation" to see a detailed, step-by-step explanation of how Herbie did it. For now, though, let's move on to look at another alternative.

The fifth alternative suggested by Herbie is much less accurate, but it is about twice as fast as the original program:

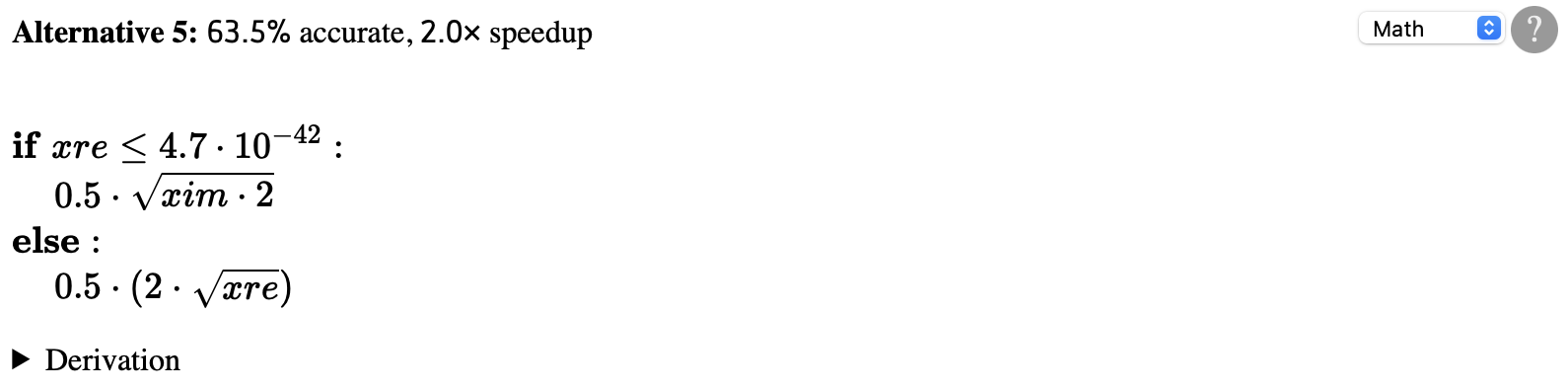
This alternative is kind of strange: it has two branches, and each one only uses one of the two variables xre and xim. That explains why it's fast, but it's still more accurate than the initial program because it avoids cancellation and overflow issues that plagued the original.

Using Herbie's alternatives

In this case, we were interested in the most accurate possible implementation, so let's try to use Herbie's most accurate alternative.

// Herbie 2.1 for:
//   0.5 * sqrt(2.0 * (sqrt(xre*xre + xim*xim) + xre))
var r = Math.hypot(x.re, x.im);
var re;
if (xre + r <= 0) {
    re = 0.5 * Math.sqrt(2 * (x.im / (x.re / x.im) * -0.5));
} else {
    re = 0.5 * Math.sqrt(2 * (x.re + r));
}
if (x.im >= 0) {
  return new Complex(
      re,
      0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}
else {
  return new Complex(
      0.5 * Math.sqrt(2.0 * (r + x.re)),
      -0.5 * Math.sqrt(2.0 * (r - x.re))
  );
}

Note that I've left the Herbie query in a comment. As Herbie gets better, you can re-run it on this original expression to see if it comes up with improvements in accuracy.

By the way, for some languages, including JavaScript, you can use the drop-down in the top-right corner of the alternative block to translate Herbie's output to that language. However, you will still probably need to refactor and modify the results to fit your code structure, just like here.

Next steps

With this change, we've made this part of the complex square root function much more accurate, and we could repeat the same steps for the other branches and other fields in this program. You now have a pretty good understanding of Herbie and how to use it. Please let us know if Herbie has helped you, and check out the documentation to learn more about Herbie's various options and outputs.